Fibonacci Heap

A fibonacci heap consists of a collection of trees which follow min heap or max heap property. In a fibonacci heap, a node can have more than two children or no children at all. The trees are constructed in a way such that a tree of order n has at least $F\_{n+2}$ nodes in it, where $F\_{n+2}$ is the $(n+2)^{th}$ Fibonacci number

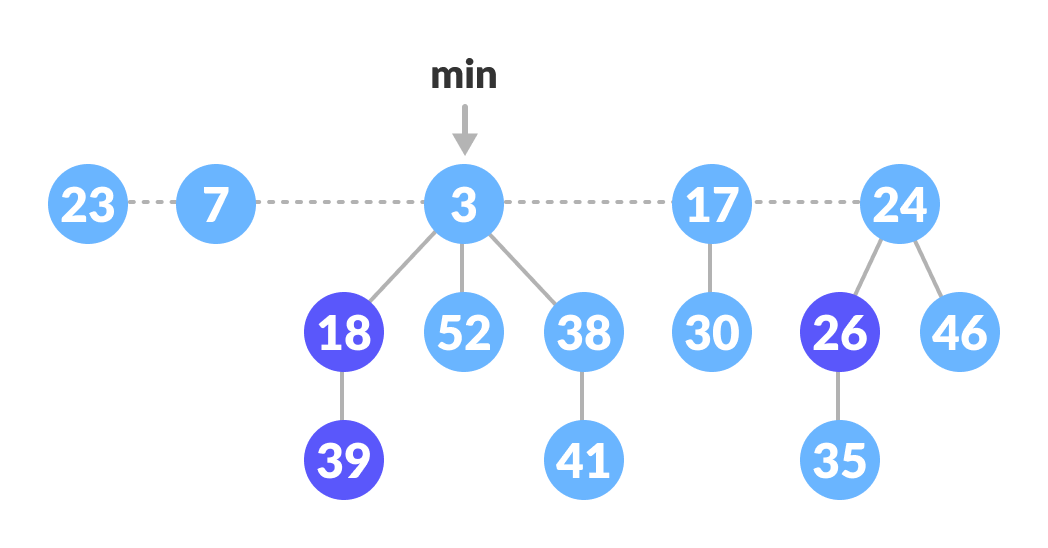
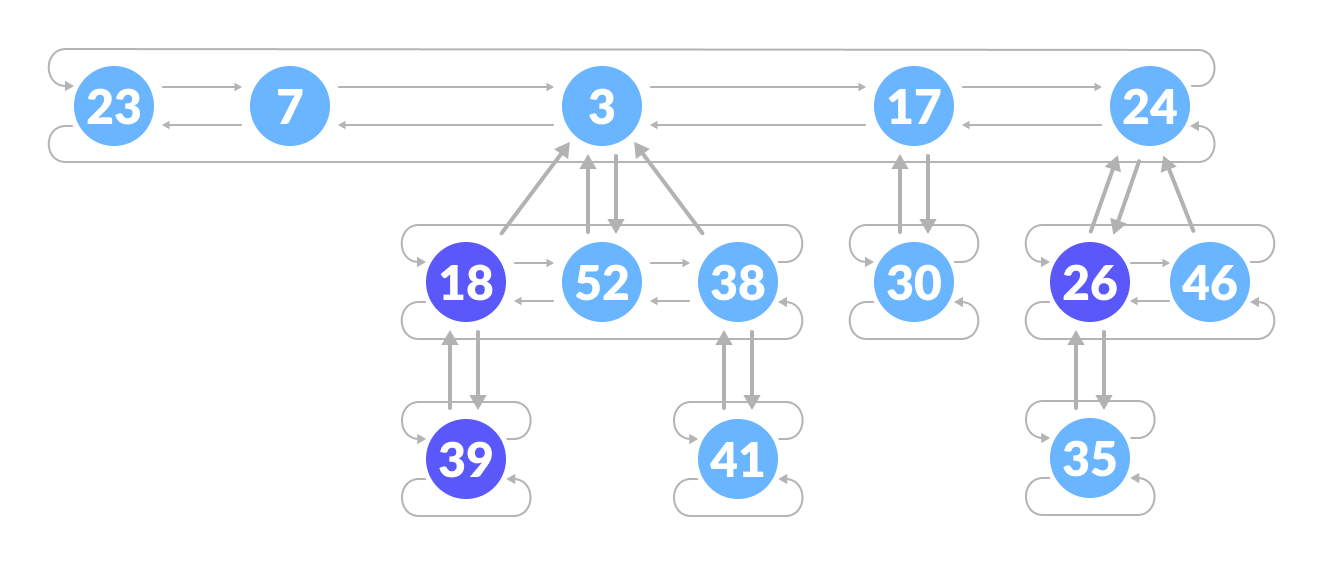
The roots of all the trees are linked together for faster access. The child nodes of a parent node are connected to each other through a circular doubly linked list. A circular doubly linked list is used because deleting a node from the tree takes O(1) time. The concatenation of two such lists takes O(1) time.

Fibonacci Heap Structure

Properties of a Fibonacci Heap

It is a set of min heap-ordered trees (I.e. the parent is always smaller than the children)
A pointer is maintained at the minimum element node
It consists of a set of marked nodes (Decrease key operation)
The trees within a Fibonacci heap are unordered but rooted

Operations

Degree of node = # of children it has (not including grand children)

Extract Min

Delete min node
Set the min-pointer to the next root in the root list
Create an array of size equal to the maximum degree of trees in the heap before deletion
Repeate (steps 5-7) until there are no multiple roots with the same degree
Map the degree of current root (min-pointer) to the degree in the array
Map the degree of next root to the degree in array
If there are more than two mappings for the same degree, then apply union operation to those roots such that the min-heap property is maintained

danger

To minimize the heights of trees after unions, we have to merge in a way such that the degree of the last tree is at most “max degree”. We should then merge trees with similar degrees which guarantees that the maximum degree will be the max degree pre-merge + 1

Max Degree

A binomial tree with degree d has $2^d$ nodes. A binomial tree with k nodes means the max degree is $log_2(k)$

Implementation

import math
 
class FibonacciTree:
	def __init__(self, val):
		self.val = val
		self.child = []
		self.degree = 0
 
	# Adding tree at the end of the tree
	def add_at_end(self, t):
		self.child.append(t)
		self.degree += 1
 
class FibonacciHeap:
	def __init__(self):
		self.trees = []
		self.least = None
		self.count = 0
 
	def insert_node(self, val):
		new_tree = FibonacciTree(val)
		self.trees.append(new_tree)
		if self.least is None or val < self.least.value:
			self.least = new_tree
		self.count += 1
 
	def get_min(self):
		if self.least:
			return self.least.value
		return None
 
	def extract_min(self):
		smallest = self.least
		if not smallest:
			return None
		for child in smallest.child:
			self.trees.append(child)
		self.trees.remove(smallest)
		if self.trees == []:
			self.least = None
		else:
			self.least = self.trees[0]
			self.consolidate()
		self.count -= 1
		return smallest.value
 
	def consolidate(self):
		aux = (floor_log(self.count) + 1) * [None]
		while self.trees:
			x = self.trees[0]
			order = x.order
			self.trees.remove(x)
			while aux[order]:
				y = aux[order]
				if x.value > y.value:
					x, y = y, x
				x.add_at_end(y)
				aux[order] = None
				order += 1
			aux[order] = x
 
		self.least = None
		for k in aux:
			if k:
				self.trees.append(k)
				if not self.least or k.value < self.value:
					self.least = k
 
	# Returns mantissa and exponent as a pair (m, e) value of a given number x.
	def floor_log(x):
		return math.frexp(x)[1] - 1
				
 
fibonacci_heap = FibonacciHeap()
 
fibonacci_heap.insert_node(7)
fibonacci_heap.insert_node(3)
fibonacci_heap.insert_node(17)
fibonacci_heap.insert_node(24)
 
print('the minimum value of the fibonacci heap: {}'.format(fibonacci_heap.get_min()))
 
print('the minimum value removed: {}'.format(fibonacci_heap.extract_min()))

Optimizations

Optimized Complexity

Time Complexity

Operation	Complexity
Insertion	O(1)
Find Min	O(1)
Union	O(1)
Extract Min	O(logn)
Decrease Key	O(1)
Delet eNode	O(logn)

Space Complexity

Heap-Implementation Indexed-D-ary-Heap Indexed-Priority-Queue-(IPQ)

Dynamic Arrays Hashmaps