Count Sort

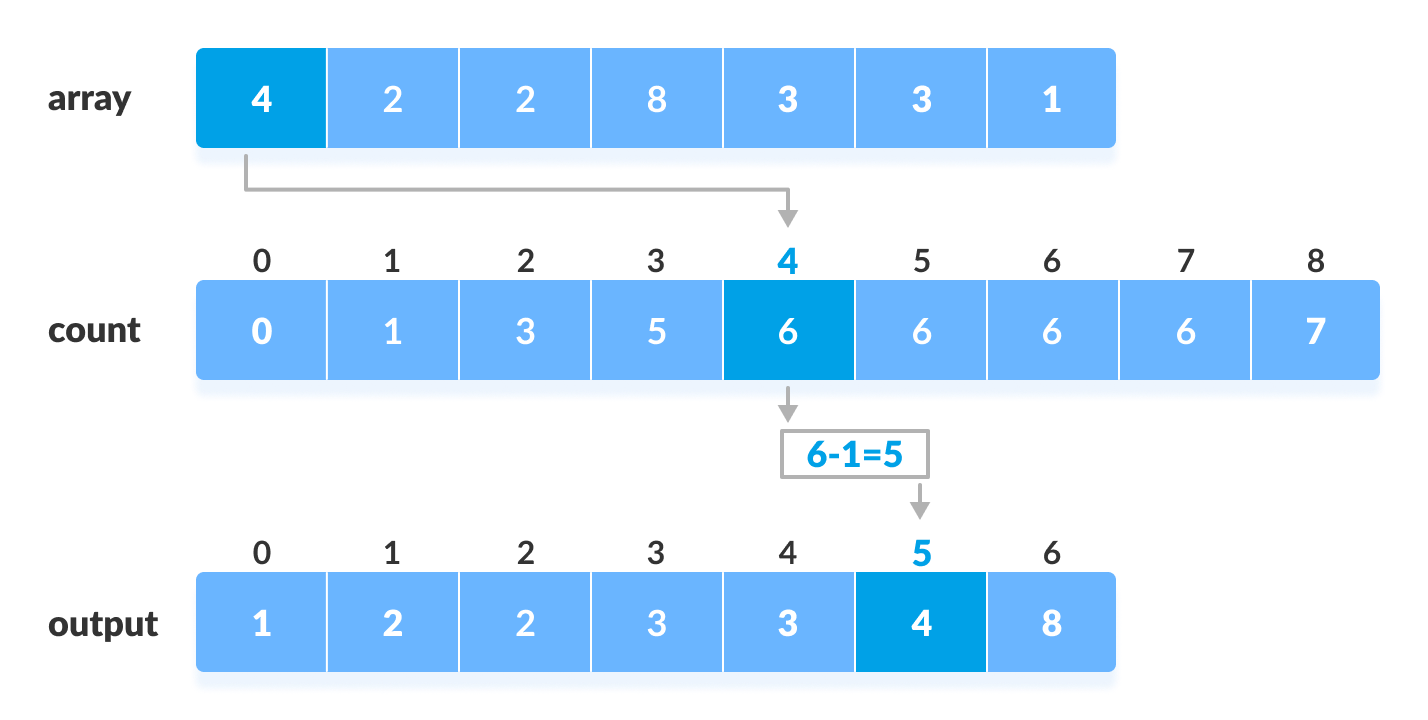
Stable sort. Count occurrences of each unique element in array and stores it in an auxiliary array. Then calculate the cumulative sum of the elements of the count array. Use the cumulative sum to place the numbers in the correct position.

note

Count sort is only really viable, time complexity less than O( $n\\log n$ ) if the length of the frequency map used is bounded by O( $n$ )

Implementation

Unstable version (without cumulative sum), works only for integers

# Saves space but doing lots of addition/subtraction
def counting_sort(nums):
	min_val = math.inf
	max_val = -math.inf
	for val in nums:
		if val < min_val:
			min_val = val
		if val > max_val:
			max_val = val
 
	sz = max_val - min_val + 1
	b = [0] * sz
	for i in range(len(nums)):
		b[nums[i] - min_val] += 1
	k = 0
	for i in range(sz):
		while b[i] > 0:
			b[i] -= 1
			nums[k] = i + min_val
			k += 1
			
# if min_val is low
def count_sort(nums):
	n = len(nums)
	# b = buckets of nums
	b = [0] * (max(n)+1)
 
	# store count
	for i in range(n):
		b[nums[i]] += 1
	
	k = 0
	for i in range(max(n)+1):
		while b[i] > 0:
			b[i] -= 1
			nums[k] = nums[i]
			k += 1

Stable version (uses cumulative sum, useful when items sorted are not just integers)

This version is stable because we iterate the unsorted array backwards, check its position in the sorted array according to the counts array, and copy it to the sorted array
The counts array is not used to tell how many times an integer appears in the unsorted array, instead, it is used to tell which position the element should be in the final sorted array. And since we decrease the count every time we output an element, we are essentially making the elements with same key’s next appearance final position smaller. That’s why we need to iterate the unsorted array from backwards to ensure its stableness. (https://stackoverflow.com/questions/2572195/how-is-counting-sort-a-stable-sort)

def counting_sort(nums):
	n = len(nums)
	k = max(nums) + 1
	count = [0] * k
	output = [0] * n
	
	# store count
	for i in range(n):
		count[nums[i]] += 1
 
	# store cumulative count
	for i in range(1,k):
		count[i] += count[i-1]
 
	# place nums backwards to ensure stableness
	for num in reversed(nums):
		# count[num] -=1 first because this stores the count but the index of the output is 0-based
		count[num] -= 1
		output[count[num]] = num
	return output

Accounting for negative numbers

count = [0] * max_val - min_val + 1 count[nums[i] - min_val] += 1

def counting_sort(nums):
    n = len(nums)
    min_val = min(nums)
    k = max(nums) - min_val + 1
    count = [0] * k
    output = [0]* n
    
    # store count
    for num in enumerate(nums):
        count[num - min_val] += 1
 
    # store cumulative count
    for i in range(1,k):
        count[i] += count[i-1]
 
    # place nums backwards
    for num in reversed(nums):
        count[num-min_val] -= 1
        output[count[num-min_val]] = num
    return output

Time/Space Complexity

Count sort is only linear in time complexity if $k$ is O( $n$ ), where $k$ is the length of the frequency map
Space Complexity is: O( $n$ + max_val - min_val) https://stackoverflow.com/questions/27668792/why-is-counting-sort-not-used-for-large-inputs

Frequency Map/Counting Problems

Count frequency of all elements
Loop starting from min num and increment freq[i]

Minimum Increment to Make Array Unique

https://leetcode.com/problems/minimum-increment-to-make-array-unique/description/

Frequency map of all elements
Increment duplicates repeatedly until count is 1 for that specific num

def minIncrementForUnique(self, nums: List[int]) -> int:
	n = len(nums)
	mx = max(nums)
	res = 0
	freq = [0]*(n+mx+1)
	for x in nums:
		freq[x] += 1
	for i in range(len(freq)):
		if freq[i] <= 1:
			continue
		freq[i+1] += freq[i]-1
		res += freq[i]-1
	return res

Maximum Product After K Increments

Greedily increment the smallest elements

def maximumProduct(self, nums: List[int], k: int) -> int:
	freq = Counter(nums)
	i = min(nums)
	while k > 0:
		ops = min(k, freq[i])
		freq[i] -= ops
		k -= ops
		freq[i+1] += ops
		if not freq[i]:
			del freq[i]
		i += 1
	res = 1
	for k in freq:
		for i in range(freq[k]):
			res = (res*k%(10**9+7))
	return res

Radix-Sort

Bucket Sort Cyclic Sort