Quick Sort
Divide and conquer. Unstable sort (due to the swapping). Studies show quicksort perform better on small datasets.
- Divide array into subarrays using a pivot element.
- Elements less than pivot are moved to the left, while elements greater are moved to the right
- Repeat divide and conquer until subarray contains a single element
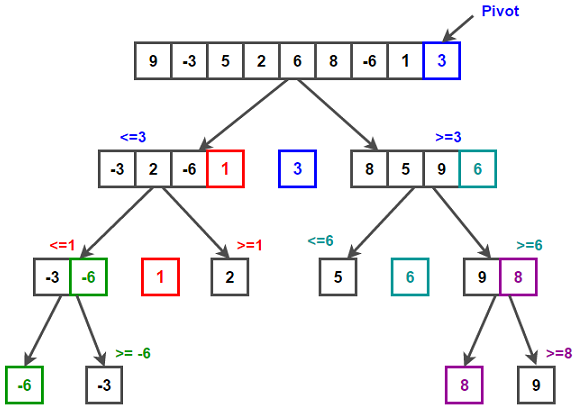
example
The pivots are picked using the rightmost element of the array each time.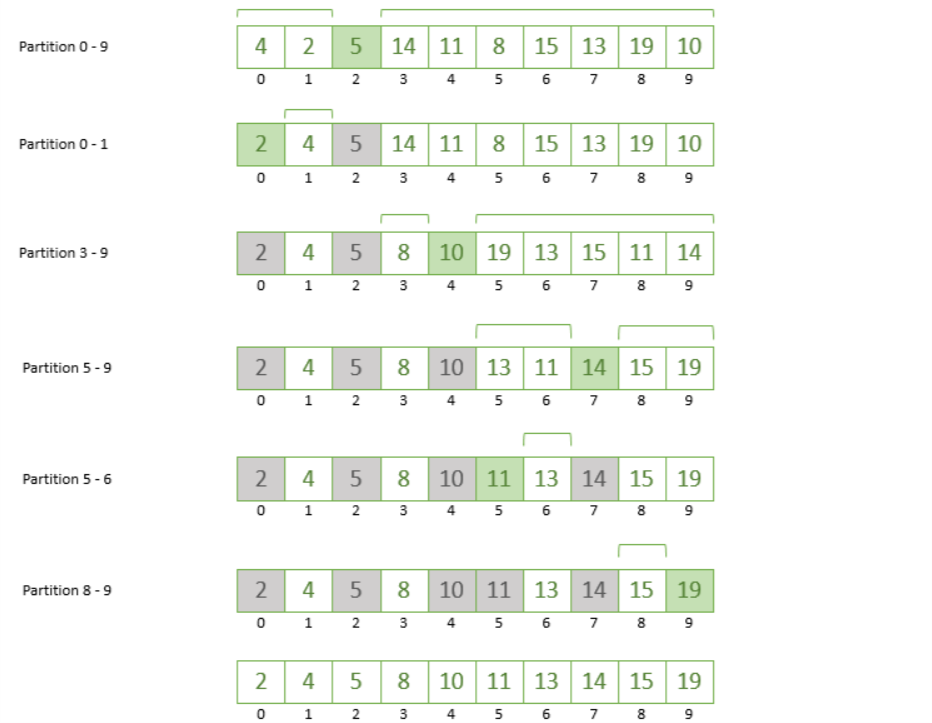
Merge Sort vs Quick Sort
Merge sort is an external sorting method in which the data that is to be sorted can be stored outside the memory and is loaded in small chunks into the memory for sorting. Quick sort is an internal sorting method, where the data that is to be sorted needs to be stored in the main memory throughout the sorting process. Thus, merge sort works better for larger datasets while quick sort works better for smaller datasets.
Implementation using Lomuto Partitioning
Lomuto Partitioning is attributed to Nico Lomuto. This works by iterating over the input array, swapping elements that are strictly less than a pre-selected pivot element. They appear earlier in the array, but on a sliding target index.
def qsort(nums: list[int]) -> None:
def qsort_helper(nums: list[int], l: int, r: int) -> None:
# Stop the partitioning when the array contains only 1 element
if l >= r:
return
p = partition(nums, l, r)
qsort_helper(nums, l, p - 1)
qsort_helper(nums, p + 1, r)
def partition(nums: list[int], l: int, r: int) -> int:
p_ind = l
pivot = nums[r]
for i in range(l, r):
if nums[i] < pivot:
nums[i], nums[p_ind] = nums[p_ind], nums[i]
p_ind += 1
nums[p_ind], nums[r] = nums[r], nums[p_ind]
return p_ind
qsort_helper(nums, 0, len(nums) - 1)Implementation with Hoare Partitioning
Hoare partitioning was proposed by Tony Hoare when the Quicksort algorithm was originally published. Instead of working across the array from low to high, it iterates from both ends at once towards the center. This means that we have more iterations, and more comparisons, but fewer swaps.
This can be important since often comparing memory values is cheaper than swapping them.
fun quicksort(input : T[], low : int, high : int)
if (low < high)
p := partition(input, low, high)
quicksort(input, low, p) // Note that this is different than when using Lomuto
quicksort(input, p + 1, high)
fun partition(input : T[], low: int, high: int) : int
pivotPoint := floor((high + low) / 2)
pivot := input[pivotPoint]
high++
low--
loop while True
low++
loop while (input[low] < pivot)
high--
loop while (input[high] > pivot)
if (low >= high)
return high
swap(input[low], input[high])Optimizations
Optimized Complexity
Time Complexity
In the worse case the complexity can reach O(n^2) if pivots are picked poorly. It has average time complexity O(nlogn).
Space Complexity