Topological Sort
- Sort the graph in an ord/er such that no vertex appears before another vertex that has an edge to it.
- The ordering does not have to be unique
Topological Sort Using DFS
- Post-Order Traversal
Run DFS on an entire graph and add each node to the global ordering of nodes, but only after all of a node’s children are visited. This ensures that parent nodes will be ordered before their child nodes, and honors the forward direction of edges in the ordering.
- Orders the vertices on a line such that all directed edges go from left to right
- Such an ordering cannot exist if the graph contains a directed cycle
- Each [[Graph Theory#Directed Acyclic Graphs (DAG)|DAG]] has at least one topological sort, they are not unique
example
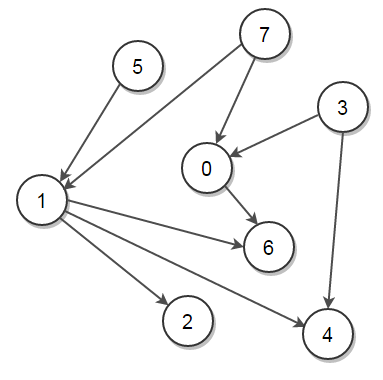
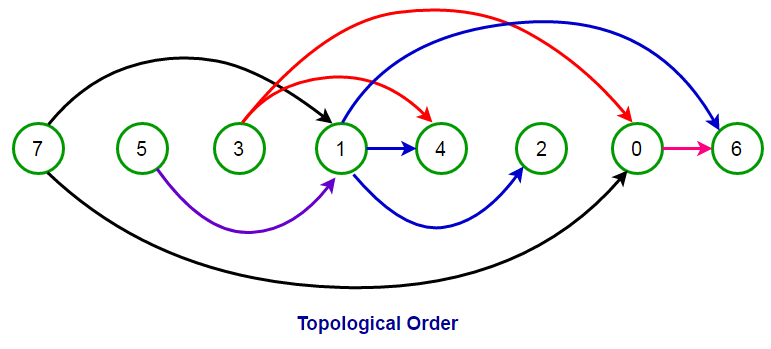
Purpose
Gives an ordering where each vertex can be processed before it’s successors. This allows us to seek the shortest/longest path from x to y in a DAG
DFS Implementation
def topsort(self,graph):
seen = set([])
ordering = deque()
for node in graph.get_vertices():
self.dfs_topsort(node, seen, ordering)
return ordering
def dfs_topsort(self, graph, node, seen, ordering):
if node in seen:
return
seen.add(node)
for neighbor in graph.get_neighbors(node):
self.dfs_topsort(neighbor, seen, ordering)
ordering.appendleft(node)Modified to detect cycles
def topsort(self,graph):
vis = defaultdict(lambda: 0)
ordering = deque()
for node in graph.get_vertices():
self.dfs_topsort(graph, node, vis, ordering)
return ordering
def dfs_topsort(self, graph, node, vis, ordering):
if vis[node] == 2:
return
if vis[node] == 1:
raise CycleError
vis[node] = 1
for nbor in graph.get_neighbors(node):
self.dfs_topsort(graph, nbor, vis, ordering)
ordering.appendleft(node)
vis[node] = 2- Time Complexity: O(V + E)
- Space Complexity: O(depth)
Kahn’s Topological Sort Algorithm
Find vertices with no incoming edges and removing all outgoing edges from these vertices.
Maintain in-degree information of all graph vertices.
Removing an edge from u to v will decrement indegree[u] by 1.
If a cycle exists, then not all vertices will be able to achieve an indegree of 0. If the top_order does not have a length of n, then we must have encountered a cycle.
def topsort(edges, n):
top_order = deque()
indegree = [0] * n
adj_list = [[] for _ in range(n)]
for u,v in edges:
adj_list[u].append(v)
indegree[v] += 1
# Store all the nodes with no incoming edges
q = deque([i for i in range(n) if indegree[i] == 0])
while q:
# extract front of queue
u = q.popleft()
# add the current vertex to the tail of the ordering
top_order.append(u)
for v in adj_list[u]:
indegree[v] -= 1
if indegree[v] == 0:
q.append(v)
if len(top_order) != n:
print('Cycle Exists')
return top_order
Applications
Use topological sort when there is a dependency on the edges
DAG Scheduling
https://leetcode.com/problems/parallel-courses-ii/description/
class Solution:
def minNumberOfSemesters(self, n: int, relations: List[List[int]], k: int) -> int:
in_degrees = [0]*n
graph = defaultdict(list)
for u,v in relations:
in_degrees[v-1] += 1
graph[u-1].append(v-1)
@lru_cache(None)
def dfs(mask, in_degrees):
if not mask:
return 0
# nodes that can be taken (if bit is 1)
nodes = [i for i in range(n) if mask & 1 << i and in_degrees[i] == 0]
ans = math.inf
# Check all combinations with size k
for k_nodes in combinations(nodes, min(k, len(nodes))):
new_mask, new_in_degrees = mask, list(in_degrees)
# set bit for all nodes in combination
for node in k_nodes:
new_mask ^= 1 << node
for child in graph[node]:
new_in_degrees[child] -= 1
# recurse
ans = min(ans, 1+dfs(new_mask, tuple(new_in_degrees)))
return ans
return dfs((1<<n)-1, tuple(in_degrees))Parallel Courses II
- Without the requirement
k, this would be a topological problem - Why do we need DP? There is no optimal subproblem on which course should be taken first.
[[LC-207. Course Schedule]] [[LC-210. Course Schedule II]]
All Ancestors of a Node in a Directed Acyclic Graph
- To guarantee sorted order of ancestors (without sorting the answer), iterate in sorted order
- Skip the next node if it has already been visited before
def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
graph = [[]for _ in range(n)]
for u,v in edges:
graph[u].append(v)
ans = [[]for _ in range(n)]
def dfs(u, par):
for v in graph[u]:
if ans[v] and ans[v][-1] == par:
continue
ans[v].append(par)
dfs(v,par)
for u in range(n):
dfs(u,u)
return ansScheduling
Find All Possible Recipes from Given Supplies
def findAllRecipes(self, recipes: List[str], ingredients: List[List[str]], supplies: List[str]) -> List[str]:
available = set(supplies)
ans, ingredient_to_recipe, in_degree = [], defaultdict(set), Counter()
for rcp, ingredient in zip(recipes, ingredients):
non_available = 0
for ing in ingredient:
if ing not in available:
non_available += 1
ingredient_to_recipe[ing].add(rcp)
if non_available == 0:
ans.append(rcp)
else:
in_degree[rcp] = non_available
for rcp in ans:
for recipe in ingredient_to_recipe.pop(rcp, set()):
in_degree[recipe] -= 1
if in_degree[recipe] == 0:
ans.append(recipe)
return ans