Combinatorics

• https://leetcode.com/problems/count-collisions-of-monkeys-on-a-polygon/description/

• There are n monkeys at pos i in an array.

• Each monkey must move once

• If they move in opposite directions, a collision happens.

• Return the number of collisions

• Is it easier to count the number of collisions or no collisions?

• No collisions = 2 for any n, because monkeys can all move cw or ccw

• Situations with collisions = $2^n - 2$

• https://leetcode.com/problems/unique-paths/solutions/504514/unique-paths/

• In other words, we’re asked to compute in how many ways one could choose p elements from p+k elements. In mathematics, that’s called binomial coefficients

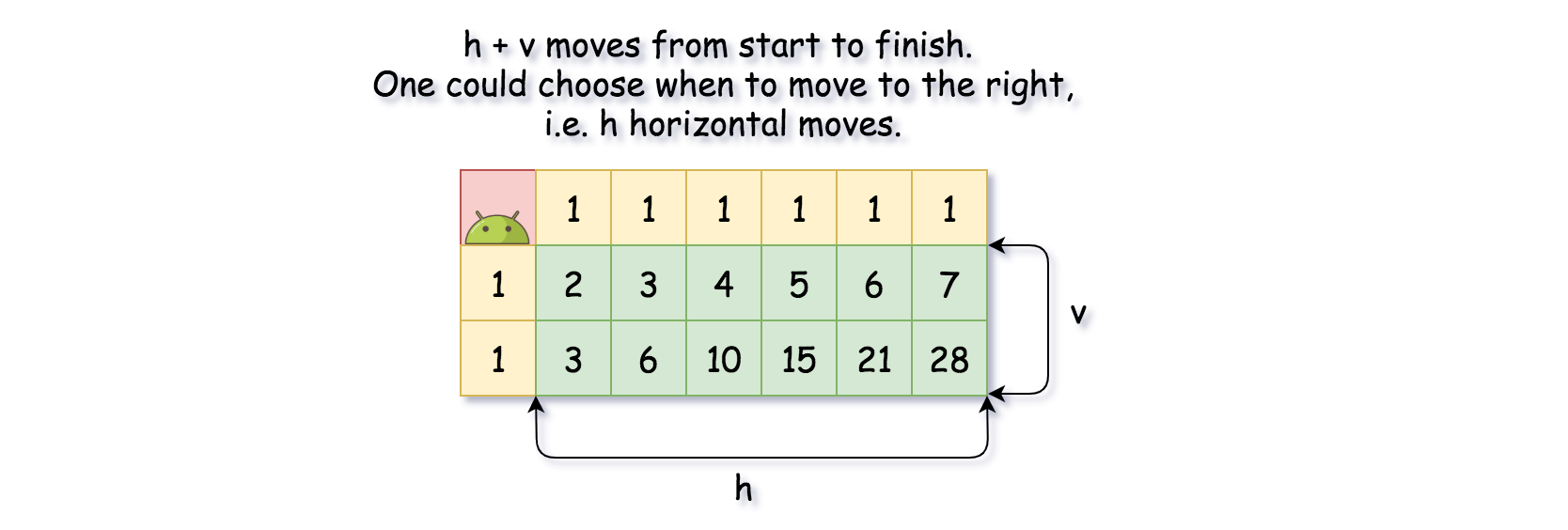
• The problem is a classical combinatorial problem: there are h+v moves to do from start to finish, h=m−1 horizontal moves, and v=n−1 vertical ones. One could choose when to move to the right, i.e. to define h horizontal moves, and that will fix vertical ones. Or, one could choose when to move down, i.e. to define v vertical moves, and that will fix horizontal ones.

• https://leetcodethehardway.com/tutorials/math/combinatorics

DP

• Useful for aggregating multiple combinations/permutations
• Find recurrence relation with a previous state

Count number of answers ‘with some conditions’ that end in ‘X’

https://leetcode.com/problems/student-attendance-record-ii/solutions/101639/pure-math-and-easy-to-understand-python-o-n-solution/

DFS with States

https://leetcode.com/problems/student-attendance-record-ii/description/

Count in Valid Intervals

https://leetcode.com/problems/plates-between-candles/description/

Count Number of Texts

https://leetcode.com/problems/count-number-of-texts/description/

def countTexts(self, pressedKeys: str) -> int:
        n = len(pressedKeys)
        dp = [0]*(n+1)
        dp[0] = 1
        m = 10**9+7
        prev = pressedKeys[0]
        for i in range(1, n+1):
            dp[i] = dp[i-1]%m
            if i >= 2 and pressedKeys[i-1] == pressedKeys[i-2]:
                dp[i] = (dp[i] + dp[i-2])%m
                if i >= 3 and pressedKeys[i-1] == pressedKeys[i-3]:
                    dp[i] = (dp[i] + dp[i-3])%m
                    if i >= 4 and pressedKeys[i-1] == pressedKeys[i-4] and pressedKeys[i-1] in '79':
                        dp[i] = (dp[i] + dp[i-4])%m
 
        return dp[n]

Permutations and Combinations

Number of Ways to Reach a Position After Exactly k Steps

Go from start to end on an infinite number line in exactly k steps https://leetcode.com/problems/number-of-ways-to-reach-a-position-after-exactly-k-steps/description/

• We have k items -> k! orderings
• We have two types of items (left or right) which are indistinguishable -> divide by left! and right!
• This is equal to k choose left (which is equivalent to k choose right)

def numberOfWays(self, startPos: int, endPos: int, k: int) -> int:
        diff = endPos - startPos
        mod = 10**9+7
        if (k - abs(diff))%2 != 0 or abs(startPos-endPos) > k:
            return 0
        return comb(k, (k-abs(diff))//2) % mod

Counting

Count Subarrays with Exactly K ‘x’

• exactly k = (at least k) - (at least k-1)

Number of Ways to Get from Top-Left to Bottom-Right

Only down and right moves are allowed

$\\frac{(m+n-2)!}{(m-1)!(n-1)!}$ $=$ ${m+n-2}\\choose{n-1}$

Sum Vowels of All Substrings

https://leetcode.com/problems/vowels-of-all-substrings/

• For a vowel at position i, how many substrings can be made with it?
  • Group 1: There are i letters before it
  • Group 2: n-i letters after it
  • Append the ith vowel to one of the groups

def countVowels(self, word: str) -> int:
        total = 0
        vowels = set('aeiou')
        for i,c in enumerate(word):
            if c in vowels:
               total += (i+1)*(len(word)-i)
        return total

Sum Distinct Score of All Substrings

From that problem, we use the fact that each character appears in (i + 1) * (n - i) substrings. However, it does not contribute to the appeal of substrings on the left that already include that character.

• Store indices of previous occurrences of the current character

def appealSum(self, s: str) -> int:
        prev = defaultdict(lambda: -1)
        res = 0
        n = len(s)
        for i,ch in enumerate(s):
            res += (i-prev[ch]) * (n-i)
            prev[ch] = i
        return res
 

Plates Between Candles

Count plates between 2 candles for all queries

• We don’t actually have to count plates
• Number of plates between 2 candles = number of spots on the range (candle i, candle j) - number of candles in this range

def platesBetweenCandles(self, s: str, queries: List[List[int]]) -> List[int]:
        candles = [i for i,c in enumerate(s) if c == '|']
        res = []
        for a,b in queries:
            i = bisect_left(candles, a)
            j = bisect_right(candles, b)-1
            res.append(candles[j]-candles[i] - (j-i) if i < j else 0)
        return res