Range Queries
Range Sum Query
1D Prefix Sums
class NumArray:
def __init__(self, nums: List[int]):
n = len(nums)
self.prefix_sums = [0]*(n+1)
for i in range(n):
self.prefix_sums[i+1] = nums[i] + self.prefix_sums[i]
# alternative
self.prefix_sums = [0] + nums
for i in range(n):
self.prefix_sums[i+1] += self.prefix_sums[i]
def sumRange(self, left: int, right: int) -> int:
return self.prefix_sums[right+1] - self.prefix_sums[left]
2D Prefix Sums
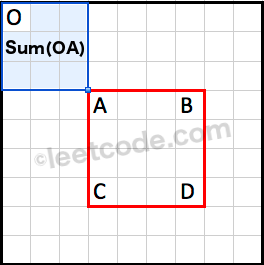
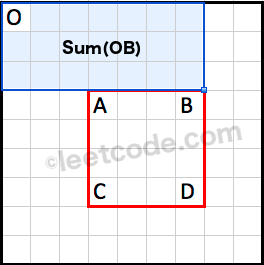
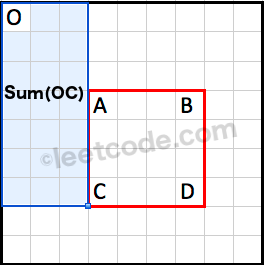 Sum(ABCD)=Sum(OD)−Sum(OB)−Sum(OC)+Sum(OA)
Sum(ABCD)=Sum(OD)−Sum(OB)−Sum(OC)+Sum(OA)
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
m, n = len(matrix), len(matrix[0])
self.sum = [[0] * (n+1) for _ in range(m+1)]
for r in range(1, m+1):
for c in range(1, n + 1):
self.sum[r][c] = self.sum[r-1][c] + self.sum[r][c-1] - self.sum[r-1][c-1] + matrix[r-1][c-1]
def sumRegion(self, r1: int, c1: int, r2: int, c2: int) -> int:
# 1-based so we can make use that dp[0][0] = 0
r1, c1, r2, c2 = r1+1, c1+1, r2+1, c2+1
return self.sum[r2][c2] - self.sum[r2][c1-1] - self.sum[r1-1][c2] + self.sum[r1-1][c1-1][[Range Minimum Query Problem]]
[[304. Range Sum Query 2D - Immutable]]
[[Fenwick (Segment) Tree]]